Construction of the Flag and the Coat of Arms of the Islamic Republic of Iran

Geometric / Algebraic Construction of the National Flag

• The ratio of the flag is officially defined to be 7:4 regardless of the designed flag ratio.
• the flag consists of three horicontal strips colored in green, white and red, which equally divide the height of the flag.
• the flag's width is made up of exactly 225 squares, which can be divided up into 3+11*(19+1)-1+3 squares, so that this defines eleven times the position of a "Allahu Akbar" pattern of width of 19 squares.
• Originally this 7x19 pattern fills out a certain fraction of the height of a (red and green) strip and so implicitly (distance of 7 squares is fixed) defined the flag's ratio to 1.7477...:1. Later this was effectively changed to exactly 1.75:1 with the consequence that the Tribar now occupies a bit more than one 7-th of a strip now.

Geometric / Algebraic Construction of the Coat of Arms

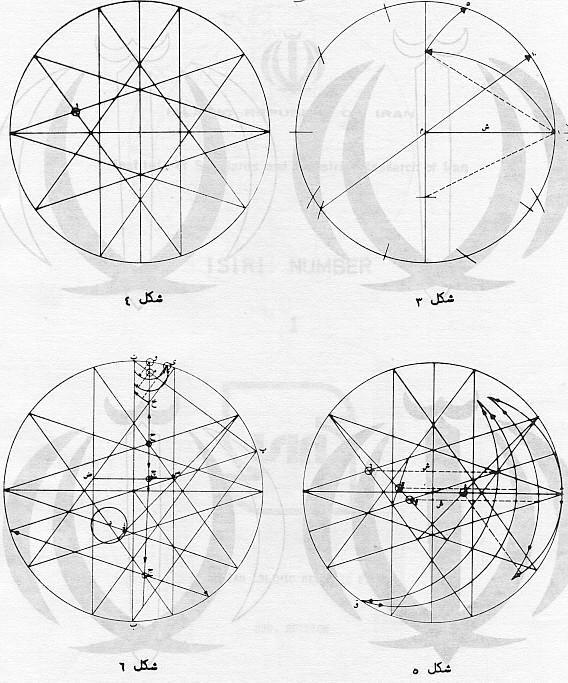
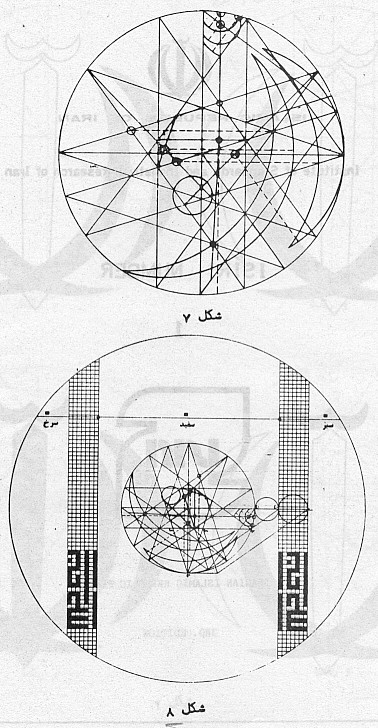
Read it form top to bottom and from right to left! The upper two pictures show the construction of the basic 10-star Lower left shows the construction of the small cresent at the top Lower right shows the construction of the two larger cresents in the emblem	Upper picture shows the construction of one half of the sword. Rotated by a quarter, the lower picture shows the precise placement and size of the Coat of Arms inside the flag.

1) positive x-axis pointing right and positive y-axis pointing down.
2) circle with radius 1 given with center in (0,0), called the "unit-circle"


Given a regular 10-star inscribing this circle. Its vertices are at Vi with
Vi := ( sin(i*Pi/10), -cos(i*Pi/10) ) and i odd:

V0 = ( 0 , -1 )
V1 = ( (sqrt(5)-1)/4 , -sqrt(10+2*sqrt(5))/4 )
V3 = ( (sqrt(5)+1)/4 , -sqrt(10-2*sqrt(5))/4 )
V4 = ( sqrt(10+2*sqrt(5))/4 , -(sqrt(5)-1)/4 )
V5 = ( 1 , 0 )
V7 = ( (sqrt(5)+1)/4 ,  sqrt(10-2*sqrt(5))/4 )
V8 = ( sqrt(10-2*sqrt(5))/4 , (sqrt(5)+1)/4 )
V9 = ( (sqrt(5)-1)/4 ,  sqrt(10+2*sqrt(5))/4 )
V10= ( 0, 1 )
V11= (-(sqrt(5)-1)/4 ,  sqrt(10+2*sqrt(5))/4 )
V13= (-(sqrt(5)+1)/4 ,  sqrt(10-2*sqrt(5))/4 )
V14= ( -sqrt(10+2*sqrt(5))/4 , (sqrt(5)-1)/4 )
V15= (-1 , 0 )
V17= (-(sqrt(5)+1)/4 , -sqrt(10-2*sqrt(5))/4 )
V19= (-(sqrt(5)-1)/4 , -sqrt(10+2*sqrt(5))/4 )

V15V3 cuts V17V9 in A    A = ( -1/2, -sqrt(10-2*sqrt(5))*(5-sqrt(5))/40 )
V17V5 cuts V11V3 in A'   A'= ( 1/2 , -sqrt(10-2*sqrt(5))*(5-sqrt(5))/40 )
Ay' = Ay = -sqrt(2-2/sqrt(5))*(sqrt(5)-1)/8 ~ -0.1624598481
Ax = -A'x
AA' = RadiusA = 1

A is center and AA' is radius of a new circle *
* cuts the unit-circle in D

V1V13 cuts V3V15 in B   B = (-3/4 + sqrt(5)/4 , (sqrt(10+2*sqrt(5))*(sqrt(5)-5) + sqrt(10-2*sqrt(5))*sqrt(5))/20 ) 
V9V17 cuts V11V19 in B ' B' = (1/4 - sqrt(5)/4 , (sqrt(10-2*sqrt(5))*(sqrt(5)-5) + sqrt(10+2*sqrt(5))*sqrt(5))/20 )
V3V11 cuts V7V15 in C'
C' = ( sqrt(5)/2 - 1 , ( sqrt(10-2*sqrt(5))*(sqrt(5)-3)+sqrt(10+2*sqrt(5))*(sqrt(5)-1) ) / 8 )
C'x ~ 0.118033988
C'y ~ 0.3632712635
BB' cuts C'V17 in C

C = ( (5-7*sqrt(5))/40 , ( sqrt(10+2*sqrt(5))*(3*sqrt(5)-5)+sqrt(10-2*sqrt(5))*(5*sqrt(5)-15) ) / 80 
Cx ~ -0.2663118960
Cy ~ -0.03102707025

Dx = ((2*sqrt(5)-5)*sqrt(65+28*sqrt(5))-5)/20
Dy = ((sqrt(5)-5)*sqrt(10-2*sqrt(5))*(1-sqrt(65+28*sqrt(5))))/80
Dx ~ -0.5481496308
Dy ~ 0.8363802862

C is center and CD is radius of a new circle @
CD = RadiusC = sqrt(530-70*sqrt(5)+(220-100*sqrt(5))*sqrt(28*sqrt(5)+65))/20
CD ~ 0.9120460695

mirror D at the line AC to get the other intersection point D'
D'x = (15*sqrt(5)-220 +(87*sqrt(5)-160)*sqrt(65+28*sqrt(5)))/620
D'y = sqrt(10-2*sqrt(5))*(163*sqrt(5)-355+(3*sqrt(5)-75)*sqrt(65+28*sqrt(5)))/2480
D'x ~ 0.3285435863
D'y ~ -0.7223844202


V9V17 cuts V5V13 in E
E = ( -C'x , C'y )
Ex ~ -0.118033988
Ey ~ 0.3632712635

V3E cuts V5V15 in F

F = ( sqrt(5)-2 , 0 )
Fx ~ 0.236067977
FV5 =  RadiusF= 3-sqrt(5)
F is the center and the distance FV5 is the radius of a new circle $

A'B' cuts V17C' in G

V5V13 cuts horizontal (parallel to V5V15 ) through G in G'

Gx = 5/22 - 2*sqrt(5)/11
Gy = ( sqrt(10-2*sqrt(5))*(sqrt(5)-15)+(7+sqrt(5))*sqrt(10+2*sqrt(5)) ) / 88
Gx ~ -0.1792850867
Gy ~ 0.05825325590
G'x = 27/22 - 2*sqrt(5)/11
G'y= Gy

G'G = RadiusG = 1
G is the center and GG' is the radius of a new circle &

F-circle and G-circle cuts in  H & H'
(Hx-Fx)^2+Hy^2=R3^2
(Hx-Gx)^2+(Hy-Gy)^2=1

Hx ~ 0.6183388412
Hy ~ 0.6614093320
H'x ~ 0.4216440014
H'y ~ -0.7410496960

V8V14 cuts V9V17 in J
Jx = sqrt(10-2*sqrt(5))/4-1/2
Jy = (10*(1+sqrt(5))+(sqrt(5)-5)*sqrt(10-2*sqrt(5)))/40
Jx ~ 0.0877852522
Jy ~ 0.6465571461

V11V19 cuts V1V13 in K
V1V9 cuts V7V19 in K'

V3V15 cuts V7V19 in I
Ix= sqrt(5)/2-1 ~ 0.118033988
Iy= -sqrt(10-2*sqrt(5))*(sqrt(5)-1)/8
Iy ~ -0.3632712640

KK' cuts vertical through I in L
Lx = Ix;
Ly = (sqrt(10-2*sqrt(5))*(5-sqrt(5))-sqrt(5)*sqrt(10+2*sqrt(5)))/20
Ly ~ -0.1004057078

IL' cuts V1V13  in M
Mx = Ix;
My = ((3*sqrt(5)-15)*sqrt(10+2*sqrt(5))+(3*sqrt(5)-5)*sqrt(10-2*sqrt(5)))/40
My ~ -0.6881909600

line from L to I ONLY above L (decrease y) until M
line from L to J ONLY below L (increase y) until N

V10V4 cuts LJ in N
Nx ~ 0.07780924870
Ny ~ 0.8929047565

V9V17 cuts V7V15 in P
P = (-3/4+sqrt(5)/4 , sqrt(10-2*sqrt(5))*(1+sqrt(5))/4/(5+sqrt(5)) )
V7V15 cuts V3E in P'

IL cuts the unit-circle at Q
RadiusQ = PP' ~ 0.1364082000
Q is the center and PP' is the radius of a new circle §
Qx = Ix ~ 0.118033988
Qy = sqrt(4*sqrt(5)-5)/2
Qy ~ -0.9930095555

Sy = ( -44*sqrt(4*sqrt(5)-5)+sqrt(1319*sqrt(5)-2933)*sqrt(5+sqrt(5)) -
      sqrt(1319*sqrt(5)-2933)*sqrt(1+1/sqrt(5)) ) / 88
Sy ~ -0.9246343081


This circle intersects the unit-circle right from Q  in T
x^2+y^2 = 1 , (x-Qx)^2 + (y-Qy)^2 = R5^2
y = (Qx^2 + Qy^2 +1 - R5^2)/2/Qy - Qx/Qy*x
4*Qy^2*x^2 + (Qx^2 + Qy^2 +1 - R5^2 - 2*Qx*x)^2 = 4*Qy^2

Tx = (2317*sqrt(5)-4615+sqrt(221770*sqrt(5)+237175)*(3-sqrt(5)))/4840
Ty = -sqrt(18235720 +sqrt(5)*9222750 + (1130-1168*sqrt(5))*sqrt(237175+221770*sqrt(5)))*(3-sqrt(5))/4840
Tx ~ 0.2520750730
Ty ~ -0.9677076818

V0V4 cuts QI  in R

R is the center and RT is the radius of a new circle #
RadiusR = RT ~ 0.1443102677
Rx = Ix ~ 0.118033988
Ry = (sqrt(10+2*sqrt(5))*(5*sqrt(5)-11)-8)/8
Ry ~ -0.914243288
S'y ~ -0.8312166012

T is the center and TU is the radius of a new circle %
RadiusT = TU ~ 0.3099945325
this circle cuts off the upper line of the swords until the center-vertical in U
Ux = 0;
Uy ~ -0.7872782843

Considering the relative size and placement of the central emblem in the National flag:

V1V5 cuts V0V10 at W'
V5V9 cuts V0V10 at W
W = ( 0 , sqrt(10+2*sqrt(5))/(5-sqrt(5)) )
W' = ( 0 , -sqrt(10+2*sqrt(5))/(5-sqrt(5)) )
==>  edge is at distance Wy ~ 1.37638192046 and thus
this is the halve of one third of the flag's total height
height of the flag ==> 3*(5+sqrt(5))*sqrt(10+2*sqrt(5))/10

For the precise height of the Takbir we need the distance between Z and Z':
Z = ( (sqrt(5)-1)/4 , sqrt(10-2*sqrt(5))*(30-10*sqrt(5))/80 )
Zx ~ 0.3090169942
Zy ~ 0.2245139883
Z' = (Zx, -Zy)
The distance ZZ' is the height of the Takbir, i.e. ZZ' = WV = W'V' in the picture.

Mirroring the drawn halve of the central emblem and filling it with red color for the flag, we get together with the two Takbir strips:

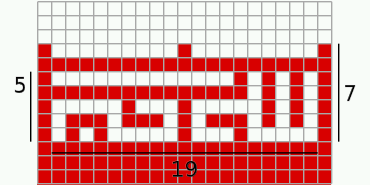
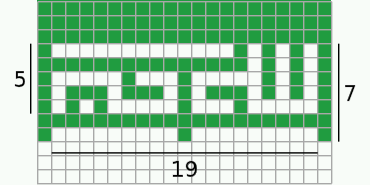
7 squares = sqrt(10-2*sqrt(5))*(30-10*sqrt(5))/40 ~ 0.44902797658
==>  flag's width = 225 squares = 45*sqrt(10-2*sqrt(5))*(30-10*sqrt(5))/56 ~ 14.43304210434381

Remark: This page sprang of a private working paper which was not intended for publication. Sorry, for the plain layout.

First time calculated on 2012-06-18.

References